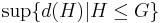Prüfer rank

In mathematics, especially in the area of algebra known as group theory, the Prüfer rank of a pro-p group measures the size of a group in terms of the ranks of its elementary abelian sections. The rank is well behaved and helps to define analytic pro-p-groups. The term is named after Heinz Prüfer.

Definition

The Prüfer rank of pro-p-group $G$ is

$\sup\{d(H)|H\leq G\}$

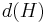where $d(H)$ is the rank of the abelian group

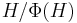$H/\Phi(H)$ ,

where 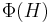$\Phi(H)$ is the Frattini subgroup of $H$ .

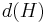As the Frattini subgroup of $H$ can be thought of as the group of non-generating elements of $H$ , it can be seen that $d(H)$ will be equal to the size of any minimal generating set of $H$ .

Properties

Those profinite groups with finite Prüfer rank are more amenable to analysis.

Specifically in the case of finitely generated pro-p groups, having finite Prüfer rank is equivalent to having an open normal subgroup that is powerful. In turn these are precisely the class of pro-p groups that are p-adic analytic - that is groups that can be imbued with a p-adic manifold structure.